Some examples of use-cases using the market models of the package
Source:vignettes/basic_usage.Rmd
basic_usage.RmdPackage diseq is deprecated. Please use package markets instead.
This short tutorial covers the very basic use cases to get you started with diseq. More usage details can be found in the documentation of the package.
Setup the environment
Load the required libraries.
library(diseq)
#> Warning: Package diseq is deprecated. Please use package markets instead.
library(magrittr)
library(Formula)Prepare the data. Normally this step is long and depends on the nature of the data and the considered market. For this example, we will use simulated data. Although we could simulate data independently from the package, we will use the top-level simulation functionality of diseq to simplify the process. See the documentation of simulate_data for more information on the simulation functionality. Here, we simulate data using a data generating process for a market in disequilibrium with stochastic price dynamics.
nobs <- 1000
tobs <- 10
alpha_d <- -0.3
beta_d0 <- 6.8
beta_d <- c(0.3, -0.02)
eta_d <- c(0.6, -0.1)
alpha_s <- 0.6
beta_s0 <- 4.1
beta_s <- c(0.9)
eta_s <- c(-0.5, 0.2)
gamma <- 1.2
beta_p0 <- 0.9
beta_p <- c(-0.1)
sigma_d <- 1
sigma_s <- 1
sigma_p <- 1
rho_ds <- 0.0
rho_dp <- 0.0
rho_sp <- 0.0
seed <- 4430
stochastic_adjustment_data <- simulate_data(
"diseq_stochastic_adjustment", nobs, tobs,
alpha_d, beta_d0, beta_d, eta_d,
alpha_s, beta_s0, beta_s, eta_s,
gamma, beta_p0, beta_p,
sigma_d = sigma_d, sigma_s = sigma_s, sigma_p = sigma_p,
rho_ds = rho_ds, rho_dp = rho_dp, rho_sp = rho_sp,
seed = seed
)Estimate the models
Prepare the basic parameters for model initialization. The simulate_data call uses Q for the simulated traded quantity, P for the simulated prices, id for subject identification, and date for time identification. It automatically creates the demand-specific variables Xd1 and Xd2, the supply-specific variable Xs1, the common (i.e., both demand and supply) variables X1 and X2, and the price dynamics’ variable Xp1.
market_spec <- Q | P | id | date ~ P + Xd1 + Xd2 + X1 + X2 | P + Xs1 + X1 + X2The market specification has to be modified in two cases. For the diseq_directional, the price variable is removed from the supply equation because the separation rule of the model can only be used for markets with exclusively either inelastic demand or supply. For the diseq_stochastic_adjustment, the right-hand side of the price dynamics equation is appended in the market specification.
By default, the models are estimated by allowing the demand, supply, and price equations to have correlated error shocks. The default verbosity behavior is to display errors and warnings that might occur when estimating the models.
By default, all models are estimated using full information maximum likelihood based on the "BFGS" optimization algorithm. The first equilibrium_model call modifies the estimation behavior and estimates the model using two stage least squares. The diseq_basic call modifies the default optimization behavior and estimates the model using the "Nelder-Mead" optimization methods.
Standard errors are by default assumed to be homoscedastic. The second equilibrium_model and diseq_deterministic_adjustment calls modify this behavior by calculating clustered standard errors based on the subject identifier, while the diseq_basic and diseq_directional calls modify it by calculating heteroscedastic standard errors via the sandwich estimator.
eq_reg <- equilibrium_model(
market_spec, stochastic_adjustment_data,
estimation_options = list(method = "2SLS")
)
eq_fit <- equilibrium_model(
market_spec, stochastic_adjustment_data,
estimation_options = list(standard_errors = c("id"))
)
bs_fit <- diseq_basic(
market_spec, stochastic_adjustment_data,
estimation_options = list(
method = "Nelder-Mead", control = list(maxit = 1e+5),
standard_errors = "heteroscedastic"
)
)
dr_fit <- diseq_directional(
formula(update(Formula(market_spec), . ~ . | . - P)),
stochastic_adjustment_data,
estimation_options = list(standard_errors = "heteroscedastic")
)
da_fit <- diseq_deterministic_adjustment(
market_spec, stochastic_adjustment_data,
estimation_options = list(standard_errors = c("id"))
)
sa_fit <- diseq_stochastic_adjustment(
formula(update(Formula(market_spec), . ~ . | . | Xp1)),
stochastic_adjustment_data,
estimation_options = list(control = list(maxit = 1e+5))
)Post estimation analysis
Summaries
All the model estimates support the summary function. The eq_2sls also provides the first-stage estimation, but it is not included in the summary and has to be explicitly asked.
summary(eq_reg@fit[[1]]$first_stage_model)
#>
#> Call:
#> lm(formula = first_stage_formula, data = object@model_tibble)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.8178 -0.9065 0.0739 0.9472 5.0795
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.64003 0.01388 262.278 <2e-16 ***
#> Xd1 0.12367 0.01385 8.932 <2e-16 ***
#> Xd2 0.02181 0.01379 1.582 0.114
#> X1 0.53012 0.01398 37.920 <2e-16 ***
#> X2 -0.14884 0.01392 -10.689 <2e-16 ***
#> Xs1 -0.41736 0.01401 -29.793 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.388 on 9994 degrees of freedom
#> Multiple R-squared: 0.2035, Adjusted R-squared: 0.2031
#> F-statistic: 510.7 on 5 and 9994 DF, p-value: < 2.2e-16
summary(eq_reg)
#> Equilibrium Model for Markets in Equilibrium
#> Demand RHS : D_P + D_Xd1 + D_Xd2 + D_X1 + D_X2
#> Supply RHS : S_P + S_Xs1 + S_X1 + S_X2
#> Market Clearing : Q = D_Q = S_Q
#> Shocks : Correlated
#> Nobs : 10000
#> Sample Separation : Not Separated
#> Quantity Var : Q
#> Price Var : P
#> Key Var(s) : id, date
#> Time Var : date
#>
#> systemfit results
#> method: 2SLS
#>
#> N DF SSR detRCov OLS-R2 McElroy-R2
#> system 20000 19989 63597.8 7.01273 -2.34127 -0.569281
#>
#> N DF SSR MSE RMSE R2 Adj R2
#> demand 10000 9994 22716.4 2.27300 1.50765 -1.38693 -1.38812
#> supply 10000 9995 40881.4 4.09018 2.02242 -3.29562 -3.29734
#>
#> The covariance matrix of the residuals
#> demand supply
#> demand 2.27300 -1.51138
#> supply -1.51138 4.09018
#>
#> The correlations of the residuals
#> demand supply
#> demand 1.00000 -0.49568
#> supply -0.49568 1.00000
#>
#>
#> 2SLS estimates for 'demand' (equation 1)
#> Model Formula: Q ~ P + Xd1 + Xd2 + X1 + X2
#> <environment: 0x5572a6361a00>
#> Instruments: ~Xd1 + Xd2 + X1 + X2 + Xs1
#> <environment: 0x5572a6361a00>
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 8.1383652 0.1336294 60.90249 < 2.22e-16 ***
#> P -0.7728748 0.0364677 -21.19340 < 2.22e-16 ***
#> Xd1 0.2788027 0.0156927 17.76637 < 2.22e-16 ***
#> Xd2 0.0147257 0.0150014 0.98162 0.32631
#> X1 0.6222757 0.0247058 25.18741 < 2.22e-16 ***
#> X2 -0.1095979 0.0161186 -6.79946 1.1102e-11 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.507647 on 9994 degrees of freedom
#> Number of observations: 10000 Degrees of Freedom: 9994
#> SSR: 22716.368772 MSE: 2.273001 Root MSE: 1.507647
#> Multiple R-Squared: -1.386928 Adjusted R-Squared: -1.388122
#>
#>
#> 2SLS estimates for 'supply' (equation 2)
#> Model Formula: Q ~ P + Xs1 + X1 + X2
#> <environment: 0x5572a6361a00>
#> Instruments: ~Xd1 + Xd2 + X1 + X2 + Xs1
#> <environment: 0x5572a6361a00>
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.1023863 0.5854996 0.17487 0.86119
#> P 1.4348674 0.1608244 8.92195 < 2.22e-16 ***
#> Xs1 0.9212974 0.0700887 13.14474 < 2.22e-16 ***
#> X1 -0.5480705 0.0874744 -6.26550 3.8696e-10 ***
#> X2 0.2187621 0.0316162 6.91930 4.8170e-12 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 2.02242 on 9995 degrees of freedom
#> Number of observations: 10000 Degrees of Freedom: 9995
#> SSR: 40881.386345 MSE: 4.090184 Root MSE: 2.02242
#> Multiple R-Squared: -3.295622 Adjusted R-Squared: -3.297341
summary(eq_fit)
#> Equilibrium Model for Markets in Equilibrium
#> Demand RHS : D_P + D_Xd1 + D_Xd2 + D_X1 + D_X2
#> Supply RHS : S_P + S_Xs1 + S_X1 + S_X2
#> Market Clearing : Q = D_Q = S_Q
#> Shocks : Correlated
#> Nobs : 10000
#> Sample Separation : Not Separated
#> Quantity Var : Q
#> Price Var : P
#> Key Var(s) : id, date
#> Time Var : date
#>
#> Maximum likelihood estimation
#> Method : BFGS
#> Convergence Status : success
#> Starting Values :
#> D_P D_CONST D_Xd1 D_Xd2 D_X1 D_X2 S_P
#> -0.77287 8.13837 0.27880 0.01473 0.62228 -0.10960 1.43487
#> S_CONST S_Xs1 S_X1 S_X2 D_VARIANCE S_VARIANCE RHO
#> 0.10239 0.92130 -0.54807 0.21876 2.27300 4.09018 -0.49568
#>
#> Coefficients
#> Estimate Std. Error z value Pr(z)
#> D_P -0.773054 0.03680 -21.0049 5.921e-98
#> D_CONST 8.138923 0.13410 60.6922 0.000e+00
#> D_Xd1 0.280904 0.01547 18.1592 1.085e-73
#> D_Xd2 0.002508 0.01301 0.1928 8.471e-01
#> D_X1 0.622361 0.02465 25.2478 1.197e-140
#> D_X2 -0.109567 0.01601 -6.8434 7.735e-12
#> S_P 1.435378 0.14831 9.6785 3.721e-22
#> S_CONST 0.100696 0.54024 0.1864 8.521e-01
#> S_Xs1 0.921469 0.06485 14.2095 7.994e-46
#> S_X1 -0.548316 0.08118 -6.7541 1.437e-11
#> S_X2 0.218814 0.03010 7.2702 3.590e-13
#> D_VARIANCE 2.272293 0.13186 17.2327 1.509e-66
#> S_VARIANCE 4.089835 0.75335 5.4289 5.670e-08
#> RHO -0.495957 0.04181 -11.8623 1.858e-32
#>
#> -2 log L: 60383.5
summary(bs_fit)
#> Basic Model for Markets in Disequilibrium
#> Demand RHS : D_P + D_Xd1 + D_Xd2 + D_X1 + D_X2
#> Supply RHS : S_P + S_Xs1 + S_X1 + S_X2
#> Short Side Rule : Q = min(D_Q, S_Q)
#> Shocks : Correlated
#> Nobs : 10000
#> Sample Separation : Not Separated
#> Quantity Var : Q
#> Price Var : P
#> Key Var(s) : id, date
#> Time Var : date
#>
#> Maximum likelihood estimation
#> Method : Nelder-Mead
#> Max Iterations : 100000
#> Convergence Status : success
#> Starting Values :
#> D_P D_CONST D_Xd1 D_Xd2 D_X1 D_X2 S_P
#> 0.044738 5.161505 0.178662 -0.001769 0.185406 0.015149 0.128093
#> S_CONST S_Xs1 S_X1 S_X2 D_VARIANCE S_VARIANCE RHO
#> 4.857007 0.376491 0.143151 0.021754 0.871035 0.775016 0.000000
#>
#> Coefficients
#> Estimate Std. Error z value Pr(z)
#> D_P -0.04710 0.01220 -3.86141 1.127e-04
#> D_CONST 5.96478 0.05151 115.79794 0.000e+00
#> D_Xd1 0.23523 0.01395 16.86213 8.546e-64
#> D_Xd2 -0.02331 0.01359 -1.71530 8.629e-02
#> D_X1 0.49477 0.02027 24.41089 1.311e-131
#> D_X2 -0.00153 0.01880 -0.08137 9.351e-01
#> S_P 0.36492 0.02044 17.85637 2.579e-71
#> S_CONST 4.81479 0.05047 95.39849 0.000e+00
#> S_Xs1 0.77298 0.02449 31.55999 1.308e-218
#> S_X1 -0.28517 0.02741 -10.40492 2.355e-25
#> S_X2 0.05738 0.02387 2.40392 1.622e-02
#> D_VARIANCE 0.85101 0.02030 41.92772 0.000e+00
#> S_VARIANCE 0.81718 0.02306 35.43429 5.065e-275
#> RHO 0.07948 0.04165 1.90818 5.637e-02
#>
#> -2 log L: 25178.6
summary(da_fit)
#> Deterministic Adjustment Model for Markets in Disequilibrium
#> Demand RHS : D_P + D_Xd1 + D_Xd2 + D_X1 + D_X2
#> Supply RHS : S_P + S_Xs1 + S_X1 + S_X2
#> Short Side Rule : Q = min(D_Q, S_Q)
#> Separation Rule : P_DIFF analogous to (D_Q - S_Q)
#> Shocks : Correlated
#> Nobs : 9000
#> Sample Separation : Demand Obs = 3731, Supply Obs = 5269
#> Quantity Var : Q
#> Price Var : P
#> Key Var(s) : id, date
#> Time Var : date
#>
#> Maximum likelihood estimation
#> Method : BFGS
#> Convergence Status : success
#> Starting Values :
#> D_P D_CONST D_Xd1 D_Xd2 D_X1 D_X2 S_P
#> 0.025528 5.258982 0.190255 0.002401 0.224474 0.012186 0.118691
#> S_CONST S_Xs1 S_X1 S_X2 P_DIFF D_VARIANCE S_VARIANCE
#> 4.900087 0.351146 0.175962 0.018346 0.967398 0.842610 0.769177
#> RHO
#> 0.000000
#>
#> Coefficients
#> Estimate Std. Error z value Pr(z)
#> D_P -0.282794 0.013288 -21.2811 1.698e-100
#> D_CONST 6.858767 0.057988 118.2796 0.000e+00
#> D_Xd1 0.185900 0.013316 13.9607 2.708e-44
#> D_Xd2 0.008247 0.010004 0.8244 4.097e-01
#> D_X1 0.567684 0.015732 36.0853 3.856e-285
#> D_X2 -0.086836 0.012297 -7.0617 1.645e-12
#> S_P 0.208697 0.013136 15.8877 7.705e-57
#> S_CONST 4.799437 0.047215 101.6500 0.000e+00
#> S_Xs1 0.481558 0.013321 36.1513 3.555e-286
#> S_X1 -0.005406 0.013757 -0.3929 6.944e-01
#> S_X2 0.065150 0.009496 6.8605 6.864e-12
#> P_DIFF 0.614386 0.017232 35.6539 2.052e-278
#> D_VARIANCE 1.277953 0.032092 39.8214 0.000e+00
#> S_VARIANCE 0.760055 0.013868 54.8083 0.000e+00
#> RHO 0.539373 0.022818 23.6381 1.565e-123
#>
#> -2 log L: 45914.2
summary(sa_fit)
#> Stochastic Adjustment Model for Markets in Disequilibrium
#> Demand RHS : D_P + D_Xd1 + D_Xd2 + D_X1 + D_X2
#> Supply RHS : S_P + S_Xs1 + S_X1 + S_X2
#> Price Dynamics RHS: (D_Q - S_Q) + Xp1
#> Short Side Rule : Q = min(D_Q, S_Q)
#> Shocks : Correlated
#> Nobs : 9000
#> Sample Separation : Not Separated
#> Quantity Var : Q
#> Price Var : P
#> Key Var(s) : id, date
#> Time Var : date
#>
#> Maximum likelihood estimation
#> Method : BFGS
#> Max Iterations : 100000
#> Convergence Status : success
#> Starting Values :
#> D_P D_CONST D_Xd1 D_Xd2 D_X1 D_X2 S_P
#> 0.025528 5.258982 0.190255 0.002401 0.224474 0.012186 0.118691
#> S_CONST S_Xs1 S_X1 S_X2 P_DIFF P_CONST P_Xp1
#> 4.900087 0.351146 0.175962 0.018346 0.968928 0.275093 -0.062290
#> D_VARIANCE S_VARIANCE P_VARIANCE RHO_DS RHO_DP RHO_SP
#> 0.842610 0.769177 1.600380 0.000000 0.000000 0.000000
#>
#> Coefficients
#> Estimate Std. Error z value Pr(z)
#> D_P -0.3195795 0.01407 -22.70704 3.817e-114
#> D_CONST 6.9163194 0.06554 105.52917 0.000e+00
#> D_Xd1 0.2874772 0.01236 23.24957 1.437e-119
#> D_Xd2 0.0070640 0.01187 0.59507 5.518e-01
#> D_X1 0.6064175 0.01726 35.14005 1.650e-270
#> D_X2 -0.0980891 0.01253 -7.82584 5.043e-15
#> S_P 0.6163763 0.03164 19.48246 1.547e-84
#> S_CONST 3.9961080 0.07155 55.85034 0.000e+00
#> S_Xs1 0.8989133 0.03142 28.60665 5.553e-180
#> S_X1 -0.4975437 0.03701 -13.44210 3.426e-41
#> S_X2 0.2036846 0.01678 12.13507 6.885e-34
#> P_DIFF 1.2124441 0.04061 29.85569 7.406e-196
#> P_CONST 0.8350155 0.05185 16.10489 2.357e-58
#> P_Xp1 -0.0832652 0.01505 -5.53409 3.129e-08
#> D_VARIANCE 1.0591615 0.03176 33.34430 8.811e-244
#> S_VARIANCE 1.0052351 0.06763 14.86391 5.653e-50
#> P_VARIANCE 1.0188468 0.07944 12.82489 1.190e-37
#> RHO_DS -0.0252917 0.06887 -0.36725 7.134e-01
#> RHO_DP -0.0008456 0.04714 -0.01794 9.857e-01
#> RHO_SP -0.0202279 0.05418 -0.37337 7.089e-01
#>
#> -2 log L: 45126Marginal effects
Calculate marginal effects on the shortage probabilities. Diseq offers two marginal effect calls out of the box. The mean marginal effects and the marginal effects ate the mean. Marginal effects on the shortage probabilities are state-dependent. If the variable is only in the demand equation, the output name of the marginal effect is the variable name prefixed by D_. If the variable is only in the supply equation, the name of the marginal effect is the variable name prefixed by S_. If the variable is in both equations, then it is prefixed by B_.
diseq_abbrs <- c("bs", "dr", "da", "sa")
diseq_fits <- c(bs_fit, dr_fit, da_fit, sa_fit)
variables <- c("P", "Xd1", "Xd2", "X1", "X2", "Xs1")
apply_marginal <- function(fnc, ...) {
function(fit) {
sapply(variables, function(v) fnc(fit, v, ...), USE.NAMES = FALSE)
}
}
mspm <- sapply(diseq_fits, apply_marginal(shortage_probability_marginal))
colnames(mspm) <- diseq_abbrs
# Mean Shortage Probabilities' Marginal Effects
mspm
#> bs dr da sa
#> B_P -0.100154381 -0.008859036 -0.155828672 -0.172370413
#> D_Xd1 0.057180496 0.066005139 0.058940070 0.052943279
#> D_Xd2 -0.005665398 -0.000339893 0.002614653 0.001300937
#> B_X1 0.189587066 0.068923076 0.181699873 0.203311137
#> B_X2 -0.014320520 -0.024924848 -0.048187589 -0.055576183
#> S_Xs1 -0.187895816 -0.121583902 -0.152679292 -0.165548468
spmm <- sapply(
diseq_fits,
apply_marginal(shortage_probability_marginal, aggregate = "at_the_mean")
)
colnames(spmm) <- diseq_abbrs
# Shortage Probabilities' Marginal Effects at the Mean
spmm
#> bs dr da sa
#> B_P -0.12739838 -0.0095704990 -0.195712135 -0.230149573
#> D_Xd1 0.07273474 0.0713059667 0.074025446 0.070690050
#> D_Xd2 -0.00720650 -0.0003671896 0.003283858 0.001737016
#> B_X1 0.24115855 0.0744582412 0.228204924 0.271461735
#> B_X2 -0.01821599 -0.0269265452 -0.060520929 -0.074205513
#> S_Xs1 -0.23900725 -0.1313482223 -0.191756690 -0.221040887Shortages
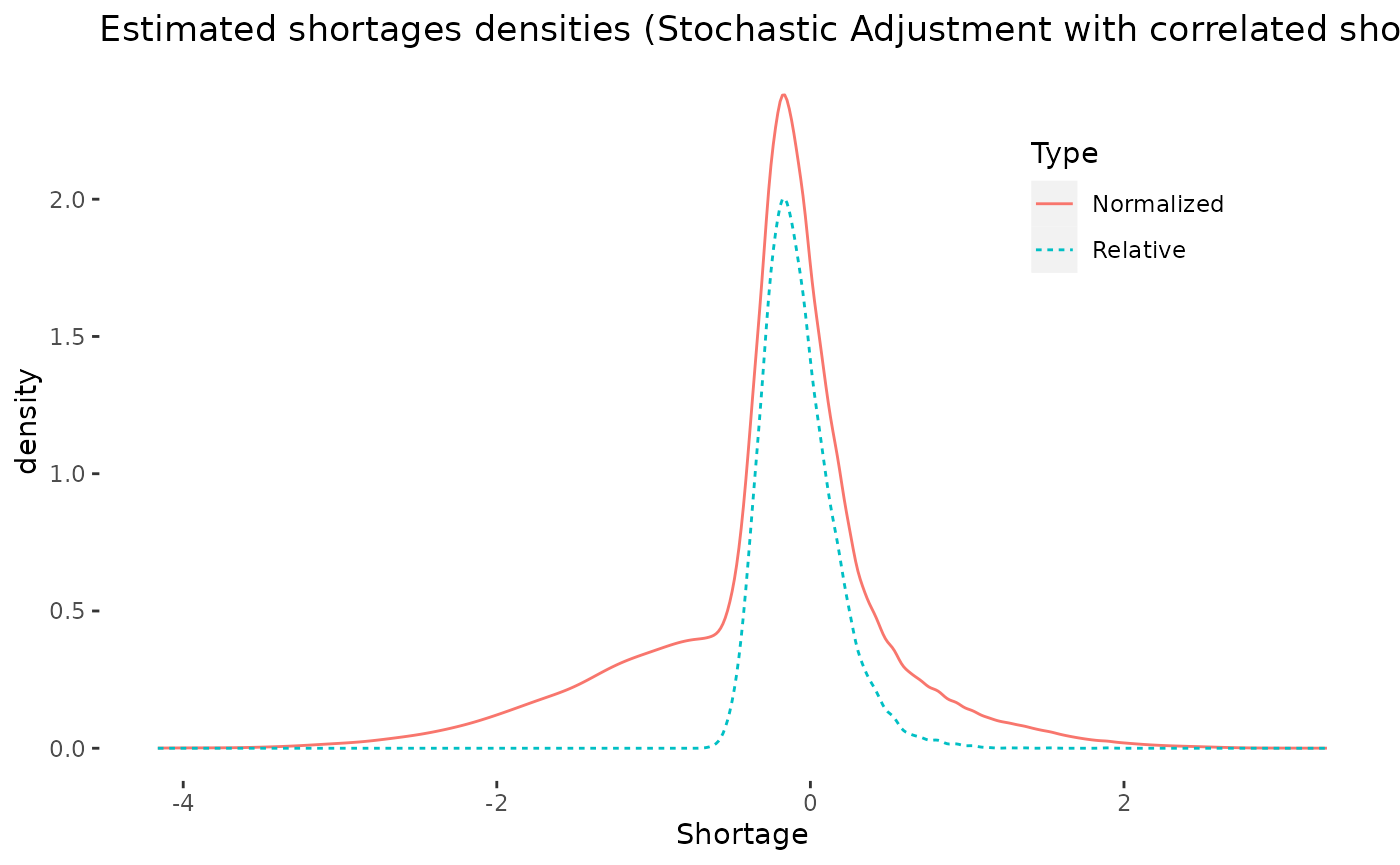
Copy the disequilibrium model tibble and augment it with post-estimation data. The disequilibrium models can be used to estimate:
Shortage probabilities. These are the probabilities that the disequilibrium models assign to observing a particular extent of excess demand.
Normalized shortages. The point estimates of the shortages are normalized by the variance of the difference of demand and supply shocks.
Relative shortages: The point estimates of the shortages are normalized by the estimated supplied quantity.
fit <- sa_fit
mdt <- tibble::add_column(
fit@model_tibble,
shortage_indicators = c(shortage_indicators(fit)),
normalized_shortages = c(normalized_shortages(fit)),
shortage_probabilities = c(shortage_probabilities(fit)),
relative_shortages = c(relative_shortages(fit))
)How is the sample separated post-estimation? The indices of the observations for which the estimated demand is greater than the estimated supply are easily obtained.
if (requireNamespace("ggplot2", quietly = TRUE)) {
pdt <- tibble::tibble(
Shortage = c(mdt$normalized_shortages, mdt$relative_shortages),
Type = c(rep("Normalized", nrow(mdt)), rep("Relative", nrow(mdt))),
xpos = c(rep(-1.0, nrow(mdt)), rep(1.0, nrow(mdt))),
ypos = c(
rep(0.8 * max(mdt$normalized_shortages), nrow(mdt)),
rep(0.8 * max(mdt$relative_shortages), nrow(mdt))
)
)
ggplot2::ggplot(pdt) +
ggplot2::stat_density(ggplot2::aes(Shortage,
linetype = Type,
color = Type
), geom = "line") +
ggplot2::ggtitle(paste0("Estimated shortages densities (", model_name(fit), ")")) +
ggplot2::theme(
panel.background = ggplot2::element_rect(fill = "transparent"),
plot.background = ggplot2::element_rect(
fill = "transparent",
color = NA
),
legend.background = ggplot2::element_rect(fill = "transparent"),
legend.box.background = ggplot2::element_rect(
fill = "transparent",
color = NA
),
legend.position = c(0.8, 0.8)
)
} else {
summary(mdt[, grep("shortage", colnames(mdt))])
}
Fitted values and aggregation
The estimated demanded and supplied quantities can be calculated per observation.
market <- cbind(
demand = demanded_quantities(fit)[, 1],
supply = supplied_quantities(fit)[, 1]
)
summary(market)
#> demand supply
#> Min. :3.175 Min. : 2.529
#> 1st Qu.:5.241 1st Qu.: 5.670
#> Median :5.684 Median : 6.366
#> Mean :5.683 Mean : 6.362
#> 3rd Qu.:6.129 3rd Qu.: 7.054
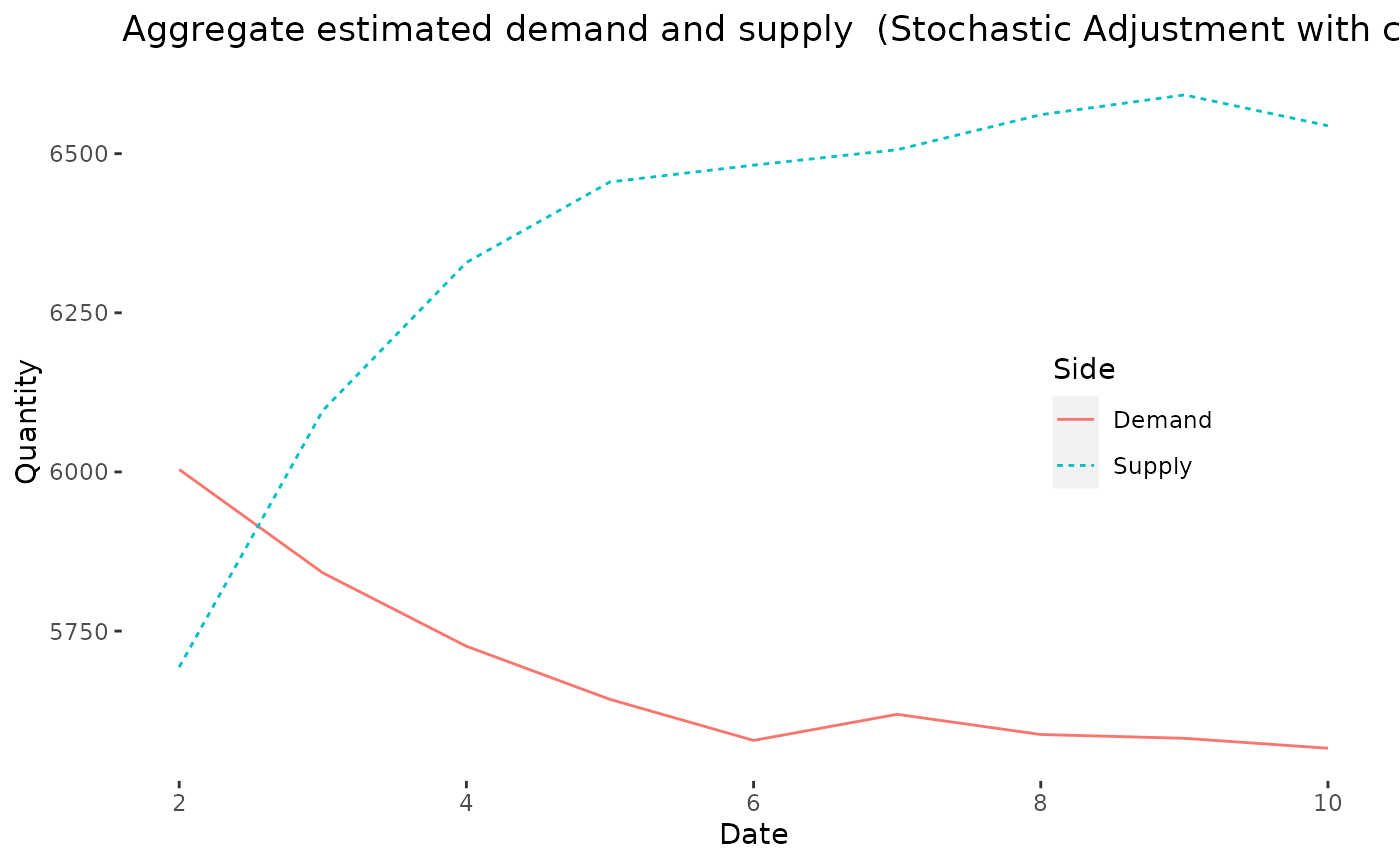
#> Max. :8.148 Max. :10.747The package also offers basic aggregation functionality.
aggregates <- aggregate_demand(fit) %>%
dplyr::left_join(aggregate_supply(fit), by = "date") %>%
dplyr::mutate(date = as.numeric(date)) %>%
dplyr::rename(demand = D_Q, supply = S_Q)
if (requireNamespace("ggplot2", quietly = TRUE)) {
pdt <- tibble::tibble(
Date = c(aggregates$date, aggregates$date),
Quantity = c(aggregates$demand, aggregates$supply),
Side = c(rep("Demand", nrow(aggregates)), rep("Supply", nrow(aggregates)))
)
ggplot2::ggplot(pdt, ggplot2::aes(x = Date)) +
ggplot2::geom_line(ggplot2::aes(y = Quantity, linetype = Side, color = Side)) +
ggplot2::ggtitle(paste0(
"Aggregate estimated demand and supply (", model_name(fit), ")"
)) +
ggplot2::theme(
panel.background = ggplot2::element_rect(fill = "transparent"),
plot.background = ggplot2::element_rect(
fill = "transparent", color = NA
),
legend.background = ggplot2::element_rect(fill = "transparent"),
legend.box.background = ggplot2::element_rect(
fill = "transparent", color = NA
),
legend.position = c(0.8, 0.5)
)
} else {
aggregates
}